Intro to Graphs
Intro
그래프(Graph) 관련 코딩테스트 문제 풀면서, 그래프 리뷰할 겸 가볍게 정리해보았습니다.
그래프 기본 개념
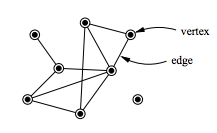
그래프는 일반적으로 막대 그래프와 같은 도표를 그리는 용어로 사용되지만, 컴퓨터 공학 분야에서는 그래프 이론에서의 그래프를 의미합니다. 그래프는 아래와 같이 객체(원으로 표시) 간의 관계(선으로 표시)를 나타냅니다.
여기서 객체는 정점(Vertex)이라고 하며, 선으로 나타낸 관계는 간선(Edge)이라고 부릅니다.
종종 정점 대신 노드(Node)라고도 하는데, 컴퓨터 공학에서 노드라는 단어를 자료 구조의 기본 단위로 사용한다고 하니(Wikipedia - Node) 편하게 일반화시켜서 부르는 것이 아닐까 예상됩니다. 그래프를 이야기하면서 노드라 칭하면 맥락 상 정점을 의미한다는 것을 주의하면 되겠습니다.
그래프 종류
그래프는 크게 무방향(Undirected) 그래프와 방향(Directed) 그래프로 나눌 수 있습니다.
무방향 그래프
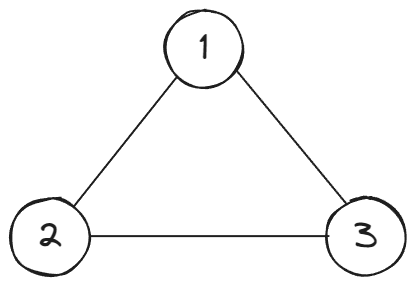
무방향 그래프는 앞서 기본 개념에서 보았던 것과 같이 정점 간에 간선은 있지만, 방향은 존재하지 않는 그래프입니다. 다시 스크롤 올리기 귀찮으니, 간단하게 무방향 그래프를 그려보자면 아래와 같습니다. 3개의 정점과 3개의 간선이 있습니다.
시험 문제로 정점이 3개인 그래프의 최대 간선의 갯수는? 하고 물어보면 n(n-1)/2 공식을 이용해서 3(3-1)/2 = 3과 같이 구할 수 있습니다.
위 그래프가 최대 간선의 갯수를 갖고 있으므로, 한 정점이 모든 정점과 연결이 되었다는 사실도 알 수 있습니다. 이러한 그래프를 완전(Complete) 그래프라고도 하며, 떨어져 있는 정점이 없으므로, 연결(Connected) 그래프라고도 할 수 있습니다.
만약 1개의 간선이 사라진다면, 완전 그래프는 아니지만 연결 그래프이기는 합니다.
방향 그래프
방향 그래프는 아래와 같이 간선에 화살표로 방향성을 표시하여 나타냅니다.
앞서 무방향 그래프에서는 양방향으로 언제든 이동할 수 있지만, 방향 그래프에서는 화살표로 표시된 방향으로만 이동할 수 있습니다.
모든 정점이 연결되어 있으므로 연결 그래프라고 할 수 있으며, 비순환 방향 그래프(Directed Acyclic Graph) 라고도 부릅니다. 한 정점에서 출발해 출발한 정점으로 다시 돌아오는 사이클(Cycle)이 존재하지 않는 방향 그래프임을 의미합니다.
앞서 무방향 그래프는 최대 간선의 갯수가 n(n-1)/2개 이지만, 방향 그래프는 모든 정점 n개가 다른 정점 n-1개 만큼 간선을 가져야 최대 간선의 갯수가 되므로 n(n-1)개 입니다. 그림으로 표현해보자면 아래와 같습니다.
기타
크게 무방향 그래프와 방향 그래프로 나누었지만, 그 속에서도 또 완전, 연결, 비순환 등의 여러 그래프로 분류할 수 있음을 살펴보았습니다.
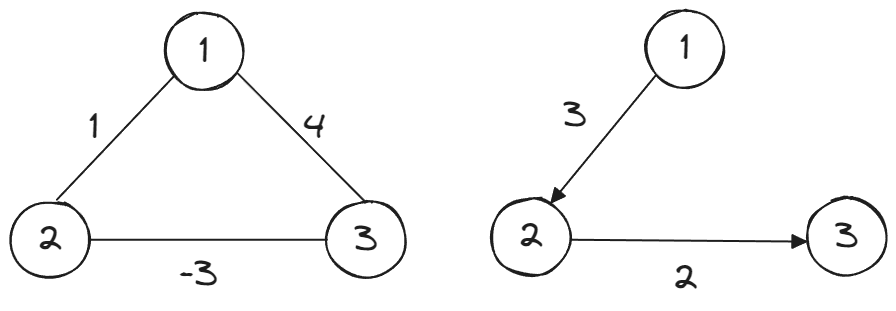
위에서 언급하지 않았지만, 중요한 그래프 종류 중 하나로 간선에 가중치가 존재하는 가중(Weighted) 그래프가 있습니다. 아래와 같이 표현할 수 있습니다.
그래프 자료구조 구현 방식
그래프 자료구조 구현 시에는 배열을 이용한 인접 배열, 리스트를 이용한 인접 리스트가 대표적이며, 파생되는 방식으로 역인접 리스트와 다중 인접 리스트도 있습니다. 여기서는 인접 배열과 인접 리스트를 살펴보겠습니다.
인접(Adjacent)
먼저 인접이라는 단어를 살펴보면, 단어 그대로 가까이 접해있는 정점을 의미합니다. 조금 더 구체적으로 정의하자면, 두 정점 사이에 간선이 존재하는 경우라 할 수 있습니다. 참고로 인접한 두 정점은 이웃(Neighbor)한다고 표현하기도 합니다.
따라서 인접 배열과 인접 리스트는 두 정점의 연결 여부 대한 정보를 저장하기 위해 배열을 사용하거나 리스트를 사용한 것입니다.
인접 배열
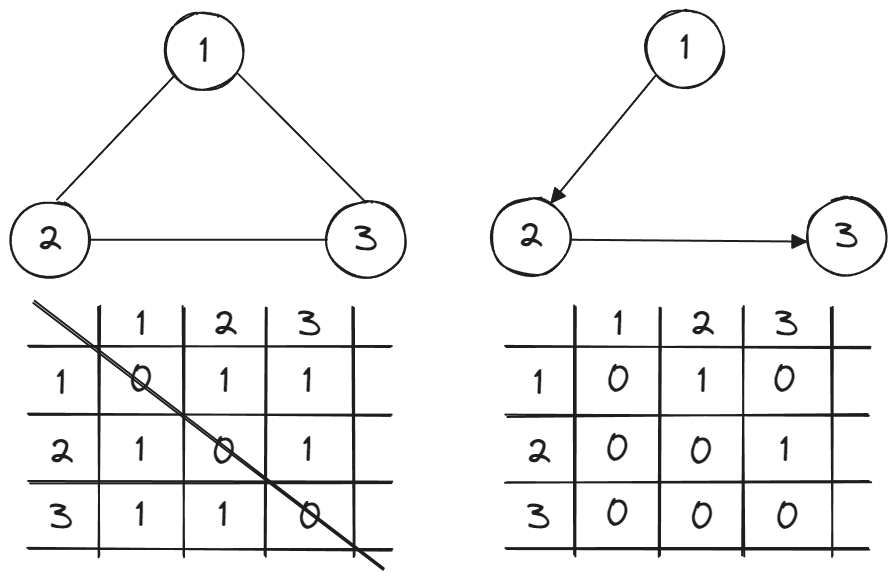
앞서 본 무방향 그래프와 방향 그래프를 각각 인접 배열로 나타내면 아래와 같습니다.
인접 배열로 나타냈을 때 무방향 그래프는 대각선으로 대칭된다는 것을 알 수 있습니다. 또한 위와 같이 정수 배열을 사용하는 경우 가중치를 표현할 수도 있습니다.
인접 리스트
마찬가지로 연결 리스트(Linked List)를 이용하여 무방향 그래프와 방향 그래프를 인접 리스트로 나타내면 아래와 같습니다.
인접 배열에서는 항상 동일한 저장공간이 필요한 반면, 인접 리스트에서는 인접한 간선에 대해서만 정보를 저장하므로, 간선의 수가 적은 희소(Sparse) 그래프의 경우 인접 리스트를 사용하는게 더 효율적일 수 있습니다.
특정 간선에 대한 정보를 조회하기 위해서는 연결 리스트이므로, 최악의 경우 특정 정점이 갖고 있는 모든 간선의 갯수인 차수(Degree)만큼 탐색이 필요하다는 단점이 있습니다. 방향 그래프의 경우에는 이러한 차수가 들어오는 방향의 간선인 경우 진입 차수, 나가는 방향의 간선인 경우 진출 차수라 합니다.
인접 배열 vs 인접 리스트 복잡도 비교
특정 간선 정보를 조회하기 위한 시간복잡도와 간선 정보를 저장하기 위한 공간복잡도 비교입니다.
| 인접 배열 | 인접 리스트 | |
|---|---|---|
| 시간복잡도 | O(1) | O(차수(v)) |
| 공간복잡도 | O(n^2) | O(n+e) |
※ 전체 정점의 갯수 = n, 전체 간선의 갯수 = e, 특정 정점 = v
그래프 탐색
대표적인 그래프 탐색 방법으로는 너비 우선 탐색(BFS, Breadth First Search)과 깊이 우선 탐색(DFS, Depth First Search)이 있습니다.
다음 사이클 없는 연결 그래프인 트리(Tree)를 예제로 BFS와 DFS를 수행하는 경우를 살펴보겠습니다.
BFS를 수행할 때 1부터 시작하는 경우 1과 인접한 2, 3을 순차적으로 방문하고, 2와 인접한 4, 5를 방문하게 됩니다. 그러면 BFS 수행 시 1, 2, 3, 4, 5 순으로 방문합니다.
DFS를 마찬가지로 1부터 시작한다면, 1의 왼쪽에 인접한 2를 방문하고, 2의 왼쪽에 인접한 4를 방문합니다. 그리고 갈 곳이 없으므로, 다시 2로 돌아온 후 인접한 5로 방문합니다. 그리고 마지막 3을 방문합니다. 정리해보면, 1, 2, 4, 5, 3 순으로 방문하게 됩니다. 예제와 같은 이진트리(Binary Tree)는 이러한 순회 방식을 전위 순회(Pre-order traversal)라고 합니다.
추상적으로는 탐색 방법이 굉장히 간단해 보입니다. 조금 더 구체적으로 인접 배열과 인접 리스트를 탐색할 때의 고려사항을 살펴보겠습니다.
인접 배열과 인접 리스트 탐색
인접 배열을 탐색한다면, 간선에 대한 정보를 수집하기 위해 각 정점에서 간선이 존재하는 배열의 위치를 찾아야 하므로, 결국 배열을 모두 탐색해야 합니다. 무방향 그래프라면 대각선 방향으로 대칭이므로, 배열의 절반만 탐색해도 되기는 합니다.
인접 배열이 특정 간선을 조회하는 속도(O(1))는 빠를지 몰라도, 그래프 탐색 시에는 희소 그래프에 가까워질수록 존재하는 간선에 대한 정보만 보관하는 인접 리스트가 더 효율적이라는 것을 알 수 있습니다.
마지막으로 두 가지 모두 공통적으로 탐색 시 필요한 것은 무한 루프에 빠지지 않도록 정점 접근 여부를 기록하는 공간이 필요하다는 점입니다.
그래프 관련 코딩테스트 문제
다양한 문제가 많이 있겠지만 최근에 풀어봤던 것들만 나열해 봤습니다.
프로그래머스
백준
Outro
간단한 내용인데 시간에만 쫓기면 왜이리 생각이 안나는지, 코딩테스트 문제를 풀면 전부 그냥 익숙한 인접 배열을 사용해서 풀었습니다. 그래프 관련 이론들을 자연스럽게 고려할 수 있도록 그래프 문제를 계속해서 더 풀어봐야겠습니다.