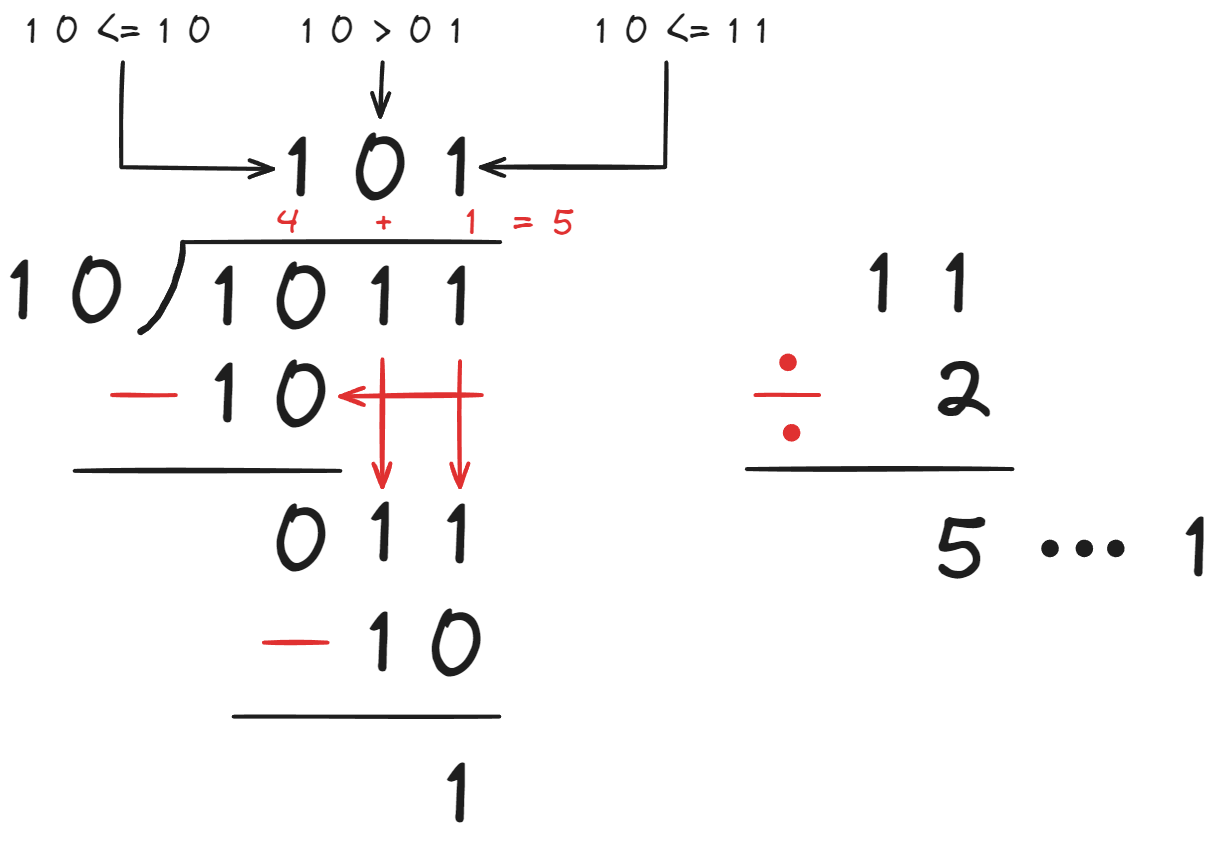
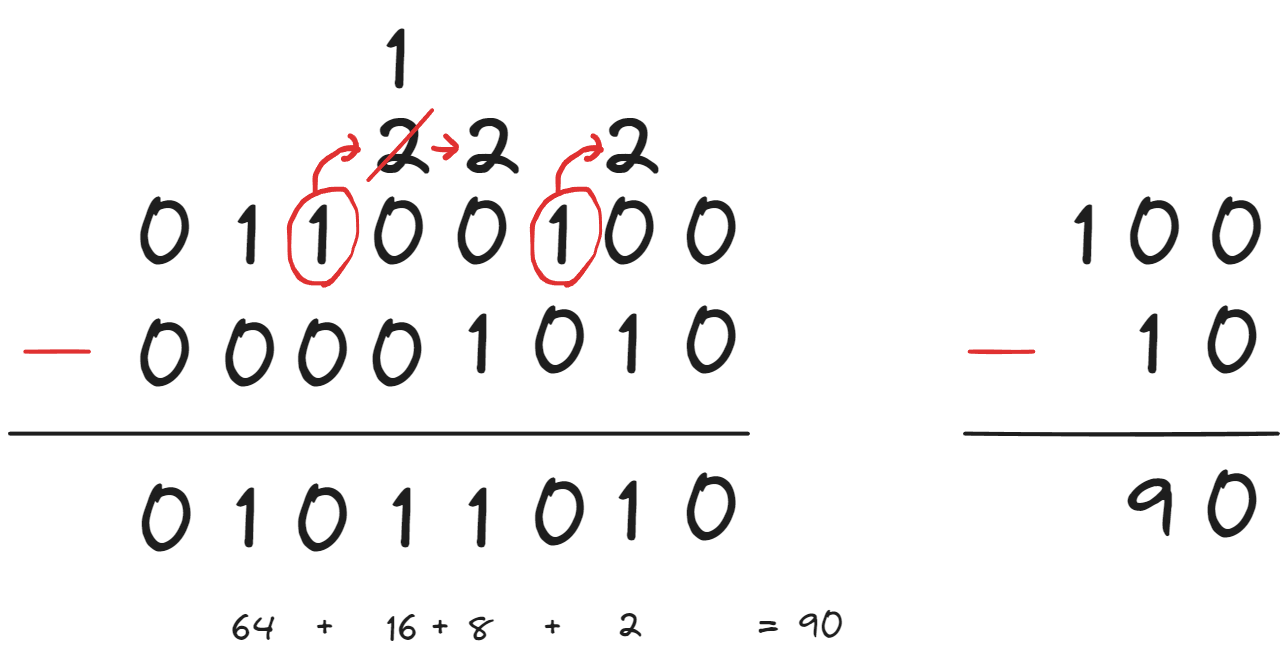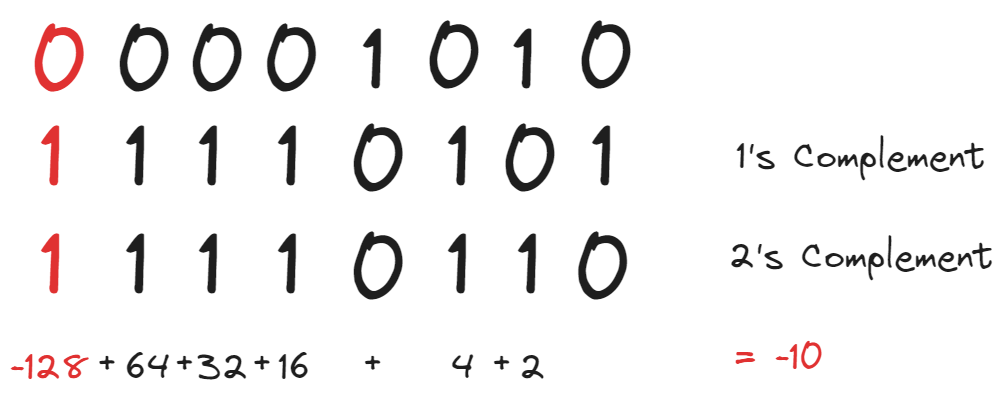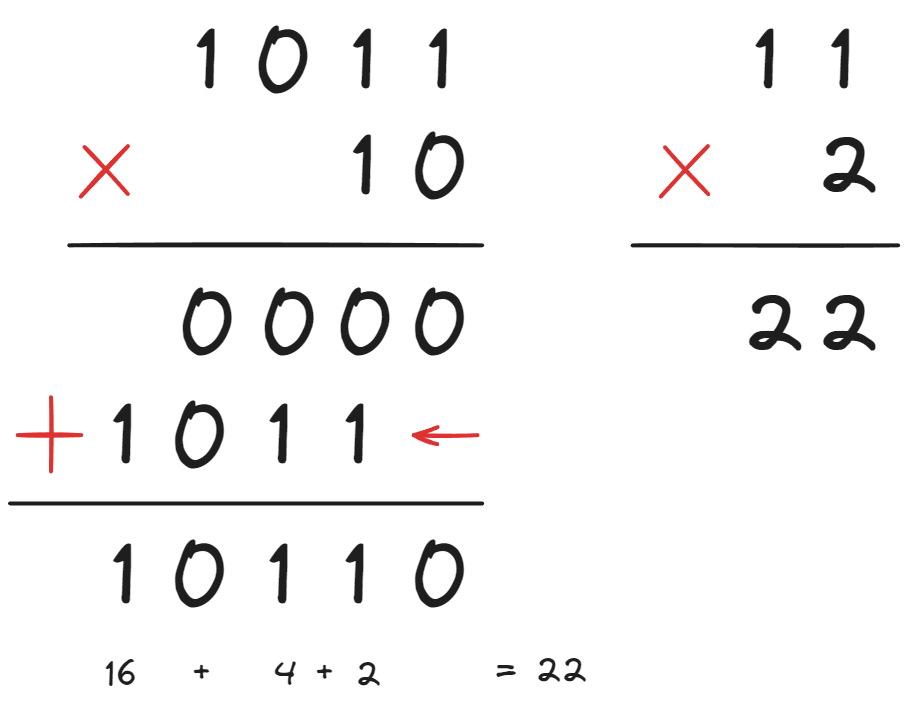컴퓨터의 사칙연산

Intro

컴퓨터의 나눗셈 연산은 상대적으로 느려서 되도록 나눗셈은 하면 안된다고 했던게 문득 생각나서, 컴퓨터는 사칙연산을 어떻게 하는지 찾아보았습니다.

덧셈 밖에 모르는 컴퓨터?

자료를 찾다보니 컴퓨터는 덧셈 밖에 못한다고 합니다. 0과 1밖에 모른다는 사실은 교양으로도 자주 볼 수 있지만, 덧셈만 가능하다는 것은 생소하게 느껴집니다.

덧셈 밖에 못하는데 어떻게 사칙연산을 할까?

덧셈은 그냥 더하면 되니까 문제가 없지만, 100에서 10을 빼려고 하는데 어떻게 더해서 뺄 수 있을까요? 당연히 머리에 떠오르신대로 100 + (-10) = 90과 같이 정수 개념을 생각해보면 음수를 더해서 뺄셈과 같은 결과를 얻을 수 있습니다.

10 x 3 과 같은 곱셈은 10 + 10 + 10 = 30 과 같이 덧셈으로 치환할 수 있습니다. 10 ÷ 3 과 같은 나눗셈은 10 에서 -3을 연속해서 더하며 -3을 더한 횟수를 카운트합니다. 그리고 10이 3보다 작아지는 경우 -3을 더하는 것을 중단하며 남은 값이 나머지가 됩니다.

하지만 컴퓨터는 0과 1밖에 모르기 때문에 2진수 연산을 해야하고, 곱셈과 나눗셈을 위와 같이 단순한 방법으로 수행하면 성능상의 문제가 발생할 수 있습니다.

사칙 연산 각각을 살펴보기 전에, 정수 연산을 수행하는 ALU(Arithmetic Logic Unit)를 먼저 간단하게 살펴보겠습니다.

ALU

ALU는 정수 사칙 연산과 논리 연산을 수행하는 장치로, 굉장히 직관적인 이름을 갖고 있습니다. 하지만 이름만으로는 유추하기 어려운 bit shift 연산을 수행하기도 합니다.

참고 자료에 따르면 부동소수점(Floating Point) 연산은 ALU가 아닌 FPU(Floating Point Unit)에서 수행합니다. 범용 CPU의 아키텍처 다이어그램(AMD 링크, INTEL 링크)을 보면, ALU는 정수 연산에 쓰이는 것을 볼 수 있지만 FPU는 다른 명칭으로 사용되는지 찾아보기 힘듭니다. 또한 ARM의 경우(링크) 부동소수점 연산 영역에 ALU가 있어 제조사마다 부르는 명칭은 달라질 수 있는 것으로 보입니다.

기본적인 ALU Symbol 살펴보기

ALU를 검색하면 쉽게 찾아볼 수 있는 Symbol과 진리표를 보면 아래와 같습니다.

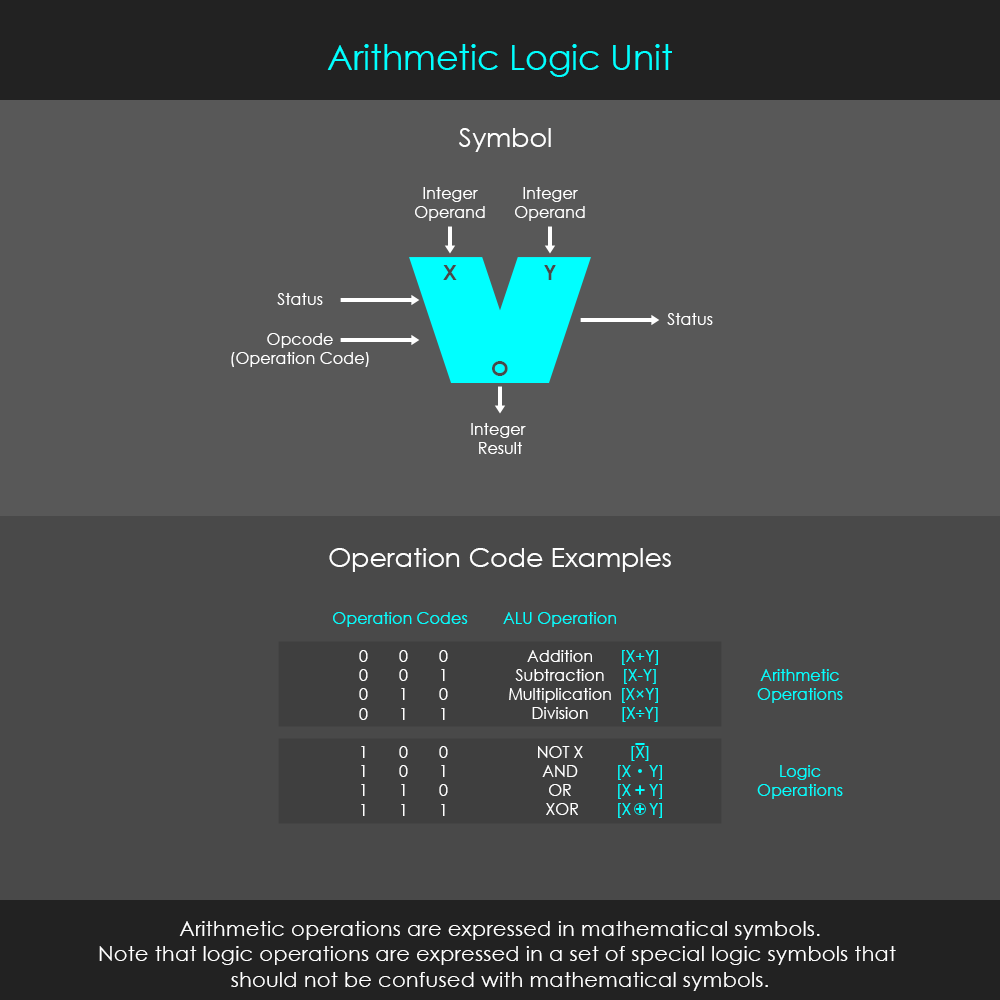
출처: exclusivearchitecture.com - Arithmetic Logic Unit(ALU)

Opcode로 연산의 종류를 지정하고, 피연산자 X, Y를 입력하여 출력 O를 얻습니다.

Wikipedia에 따르면 Status의 입력으로는 일반적으로 이전 자리수 연산을 한 ALU에서 출력한 올림수(Carry)를 받는데 사용됩니다. 그리고 범용 ALU에서 일반적으로 사용되는 출력으로는 앞서 언급한 올림수를 포함하여, 출력 비트가 모두 0인지 여부(Zero), 연산 결과가 입력의 부정인 경우(Negative), 연산 결과가 범위를 초과한 경우(Overflow), 출력에서 1인 bit의 수가 짝수인지 홀수인지 여부(Parity) 등이 있습니다.

주 관심사인 '어떻게 덧셈 하는가?' 에 대한 의문을 해결하기 위해서는 가산기(Adder)를 살펴보아야 합니다.

가산기

2진수 덧셈 연산은 아래와 같이 수행할 수 있습니다.

출처: exclusivearchitecture.com - Arithmetic Logic Unit(ALU)

그런데 컴퓨터는 0과 1밖에 모르는데, 어떻게 더한다는 동작을 할 수 있을까요?

덧셈을 위한 논리 연산

0과 1만을 이용하여 덧셈을 하기 위해 논리 연산을 수행합니다. 2진수를 더하는 것과 같은 논리 연산은 XOR 연산으로 구현할 수 있습니다. XOR은 같은 숫자일 때는 0, 다른 숫자일 때는 1을 반환하므로, 2개의 2진수를 덧셈 연산한 결과와 같습니다.

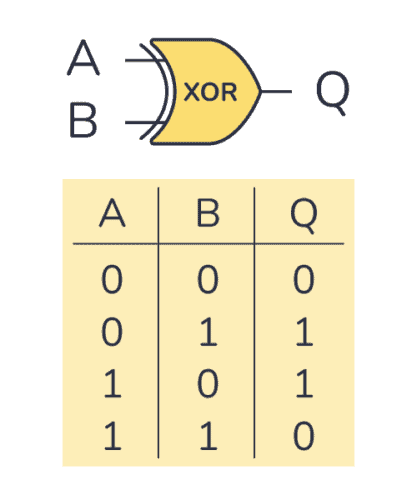
출처: build-electronic-circuits.com - XOR Gate

그런데 XOR 연산만 사용했을 때는 올림수를 알 수 없습니다. 이 문제를 해결하기 위해서는 두 수가 모두 1일 때 더하면 올림수 1이 발생하므로 AND 연산이 필요합니다.

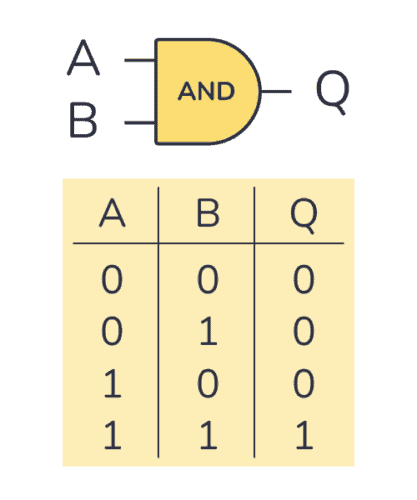
출처: build-electronic-circuits.com - AND Gate

이러한 논리 연산을 조합하여 가산기를 구성합니다. 먼저 간단한 XOR와 AND 연산을 1회씩 수행하는 반가산기(Half Adder)를 살펴보겠습니다.

반가산기

반가산기는 앞서 살펴본대로 XOR 연산을 통해 해당 자릿수의 2진수 덧셈 결과를 출력하고, AND 연산을 통해 올림수를 출력합니다.

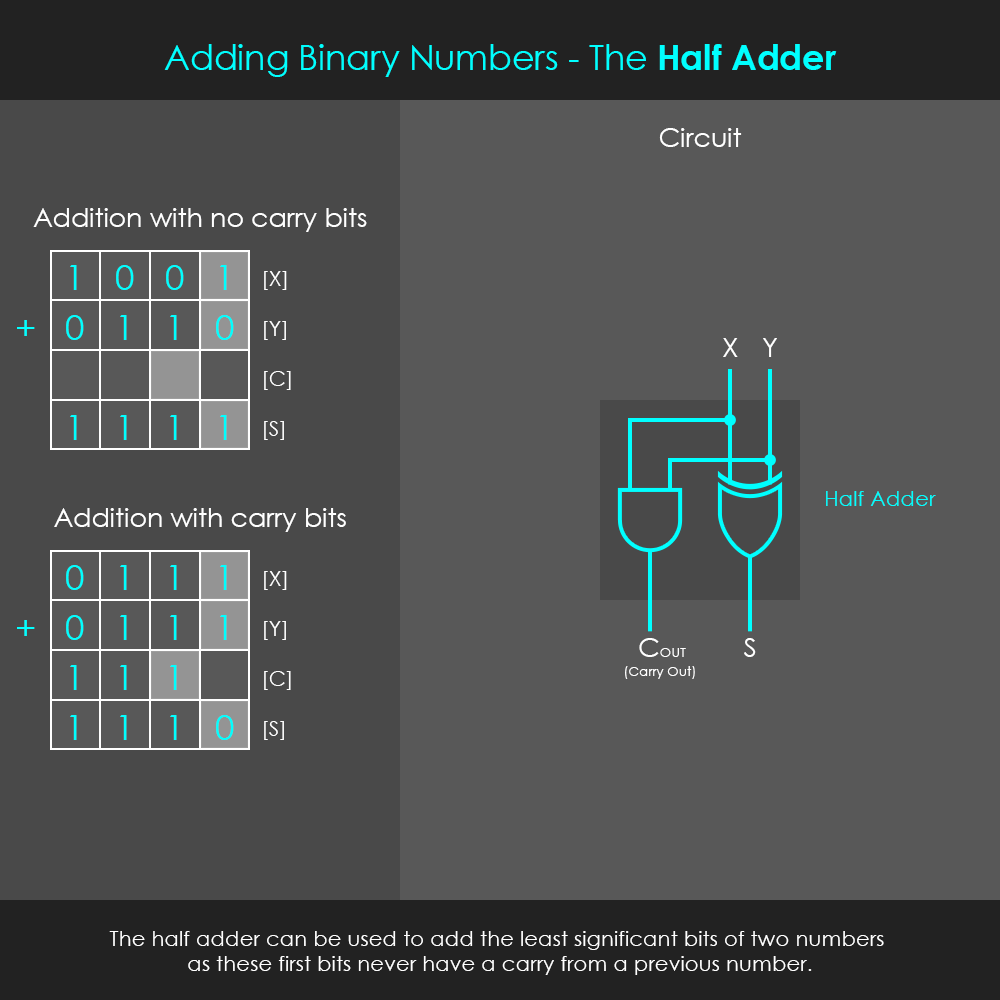
출처: exclusivearchitecture.com - Arithmetic Logic Unit(ALU)

하지만 반가산기는 올림수를 입력으로 받을 수 없기 때문에, 올림수가 필요없는 최하위 비트(LSB, Least Significant Bit)에 사용됩니다. 올림수를 입력으로 받기 위해서는 반가산기 2개를 조합한 전가산기(Full Adder)가 필요합니다.

전가산기

전가산기는 아래와 같이 입력으로 올림수를 하나의 반가산기를 더 추가해서 받고, OR 연산을 추가하여 올림수를 출력합니다.

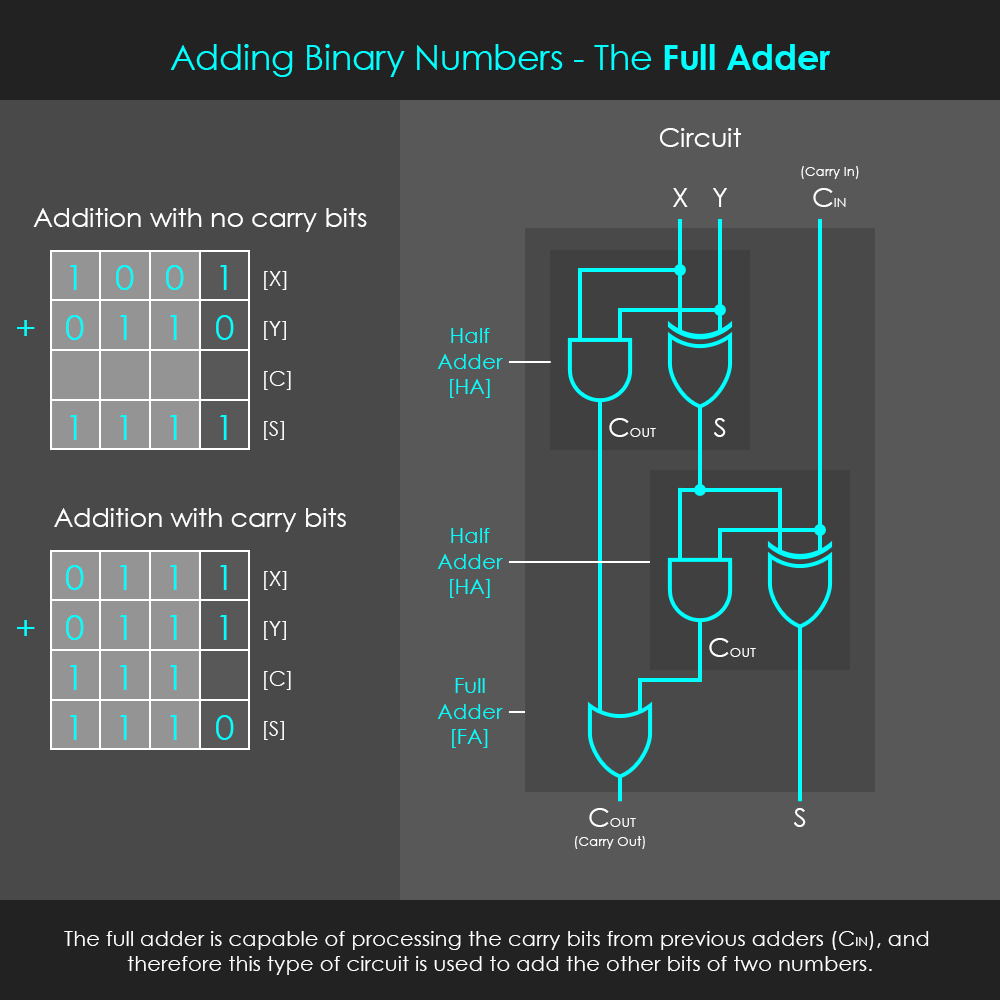
출처: exclusivearchitecture.com - Arithmetic Logic Unit(ALU)

이미지 출처로 적어둔 곳에 반가산기와 전가산기를 조합한 4 bit 가산기, 1 bit ALU 등 이미지 자료가 더 있습니다. 궁금하신 분들은 한 번 확인해 보시는 것을 추천드립니다.

이제 각각의 연산을 살펴보겠습니다.

덧셈

2진수의 덧셈 연산은 이미 가산기에서 봤으므로, 넘어가겠습니다.

뺄셈

음수 표현

앞에서 뺄셈 방법으로 음수를 더하는 것을 이야기했습니다. 컴퓨터는 0과 1밖에 모르기 때문에 0과 1로 음수를 표현해야 합니다. 음수를 표현하기 위해 최상위 비트(MSB, Most Significant Bit)를 부호 비트로 사용하여 양수면 0, 음수면 1로 표시합니다. 아래는 8bit 정수에서 최상위 비트를 부호 비트로 사용하였을 때의 값을 보여줍니다.

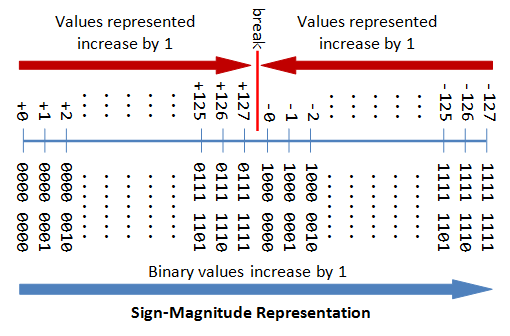
출처: Nanyang Technology University - A Tutorial on Data Representation

그런데 2진수로 표현된 +127과 -127을 더해도 0이 되지 않는다는 것은 자명해 보입니다. 원하는 결과값을 얻기위해서는 보수(Complementary Number)를 더해야 합니다.

보수

임의의 정수 x 의 보수 y 는 x + y 연산 시 자리올림이 발생하는 y의 최소값을 말합니다. 10의 보수라면 x + y = 10, 2의 보수라면 x + y = 2가 되어야 합니다.

개인적으로는 여집합(Complement of Set)의 이미지와 연관지었을 때 쉽게 이해됐습니다.

10진수

먼저 앞서 보았던 10진수 연산 100 - 10 을 보수를 이용하여 계산해 보겠습니다. 피연산자 100이 세자리 이므로, 계산하기 쉽게 010을 9의 보수로 변환하면 989가 되고, 10의 보수로 변환하기 위해 1을 더하면 990이 됩니다. 둘을 더하면 100 + 990 = 1090 이 되며, 첫 번째 자리의 올림수를 제거하면 90이 됩니다.

2진수

컴퓨터는 2진수를 사용하므로, 이번에는 100과 10을 2진수로 변환해서 계산해 보겠습니다. 보수를 사용하지 않고 2진수 뺄셈을 손으로 해보면 아래와 같습니다.

이러한 뺄셈을 구현하는 감산기 회로를 만들수도 있습니다.

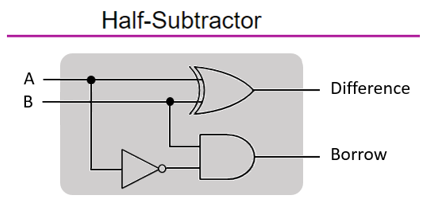
출처: 101computing.net - Binary Subtraction using Logic Gates

혹은 XOR과 AND 연산을 수행하는 것은 동일하므로, 가산기 외부에서 입력에 추가적인 논리연산을 통해 감산기로 동작하게 할 수도 있습니다.

일단은 가산기로 해결하는 방법을 살펴보기 위해, 2진수로 표현한 10을 2의 보수로 변경하는 과정을 보겠습니다.

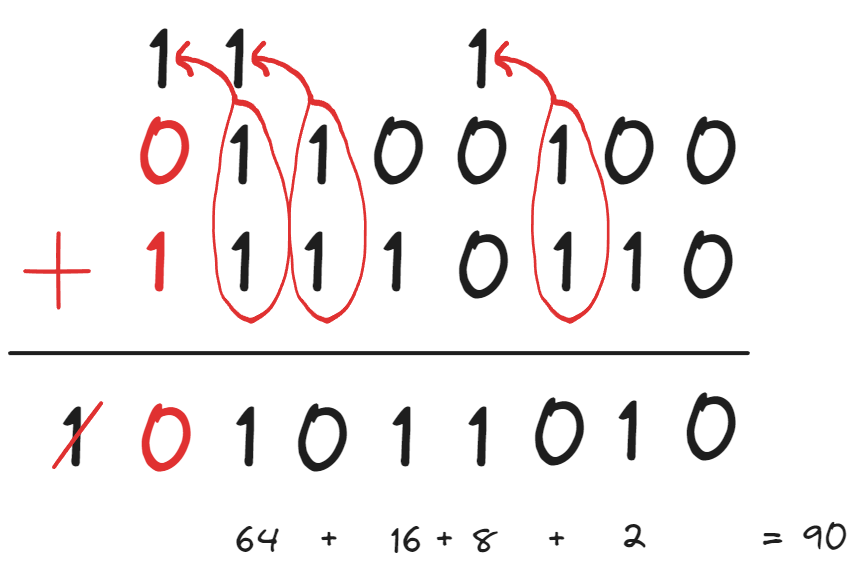
최상위 비트를 부호 비트로 사용하여 2의 보수로 표현하고, 10진수로 변환해보면 -10으로 표현 가능하다는 것을 볼 수 있습니다. 여기서 구한 2의 보수 값을 더해주면 이전과 같이 90을 얻을 수 있습니다.

2의 보수를 구하기 위해 NOT 연산을 하고, 증산기(Incrementer)로 1증가 시키면 되므로 크게 어렵지 않음을 알 수 있습니다.

곱셈

앞서 곱셈은 피연산자 값 만큼 반복해서 더하는 방식을 언급하기는 했지만, 성능상의 문제가 발생할 수 있다고도 했습니다.

최근 사용되는 범용 CPU는 보통 64bit 인데, 64자리를 모두 사용하여 2의 64제곱(=18,446,744,073,709,551,616)회 만큼 덧셈을 하는 최악의 경우를 생각해보겠습니다. 오버클럭에 성공한 10 GHz 의 CPU가 모든 자원을 덧셈에만 투자한다고 해도, 시간이 약 1,844,674,407초(= 30,744,573분 = 512,409시간) 필요합니다.

2진수의 곱셈은 손수 계산할 때 처럼 계산한다면, 위의 경우에 비해 효율적으로 계산할 수 있습니다. 아래 간단한 예제를 보겠습니다.

1과 0 밖에 없으므로, 각 자리수에 맞추어 1일 때는 피연산자를 그대로 복사해서 사용하면 됩니다. 그리고 더하기만 하면됩니다.

여기서 각 자리에 맞추는 역할을 해주는 것이 bit shift 연산입니다. shift 연산을 통해 각 자리에 맞추어 이동시킬 수 있습니다.

따라서 최악의 경우 64bit CPU는 shift 연산 64회, 더하기 64회를 통해 곱셈 결과를 얻을 수 있습니다.

나눗셈

앞서 나눗셈은 여러 번 빼는 방식을 설명드렸었습니다. 하지만 곱셈과 마찬가지로 효율적이지 못한 문제가 있습니다. 나눗셈 문제를 해결할 방법은 곱셈과 유사하게 밀고(shift), 빼면 됩니다.

나눗셈의 경우 피연산자의 자리수 차이에 따라 연산횟수가 달라지게 됩니다.

이렇게만 보면 굉장히 간단한 것 같아서 곱셈대비 나눗셈이 왜 느린지 의문이 생깁니다. 밀고 더하는 것과 밀고 빼는 것에서 왜 성능 차이가 날까요? 나눗셈을 할 때 필요한 정보들을 생각해보면 조금은 의문이 해소됩니다.

나눗셈은 몫과 나머지 값을 관리할 뿐만아니라 나누어지는지 비교 연산도 수행해야 하며, 비교 대상이 되는 수도 중간중간 새롭게 생성해야 합니다. 한마디로 그냥 해야할 작업이 많습니다.

AMD와 INTEL CPU 명령어의 Latency와 Throughput 을 측정한 자료를 보면, 과거에 비해 많이 줄어들고는 있지만 그래도 차이가 꽤 크다는 것을 볼 수 있습니다.

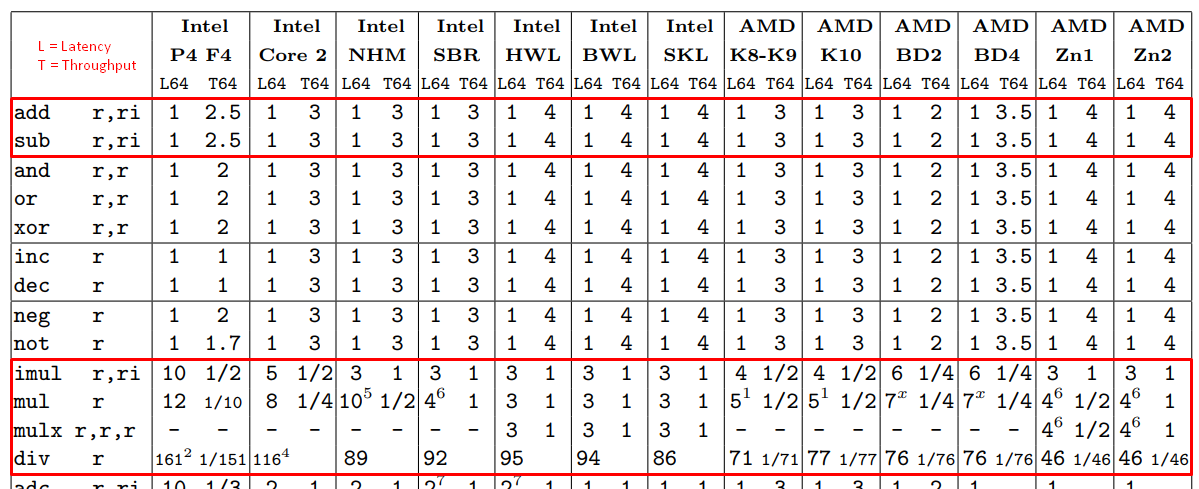
출처: gmplib.org - Instruction latencies and throughput for AMD and Intel x86 processors

Outro

컴퓨터가 사칙연산하는 방법을 살펴봤습니다. 그런데 이는 하나의 방법일 뿐 모든 컴퓨터가 동일하게 계산하지는 않습니다. 다른 수학적 방법을 이용해서 하드웨어 구현이 다를 수도 있습니다. 그래서 하드웨어 측면을 살펴보면, ARM Cortex-M3 에서는 감산기 하드웨어를 내장하고 있다고 참고자료에서 언급하고 있고, 다른 CPU 아키텍처 다이어그램을 찾아보면 IMUL, IDIV 등 곱셈과 나눗셈을 위한 별도의 하드웨어를 구현하고 있기도 합니다.

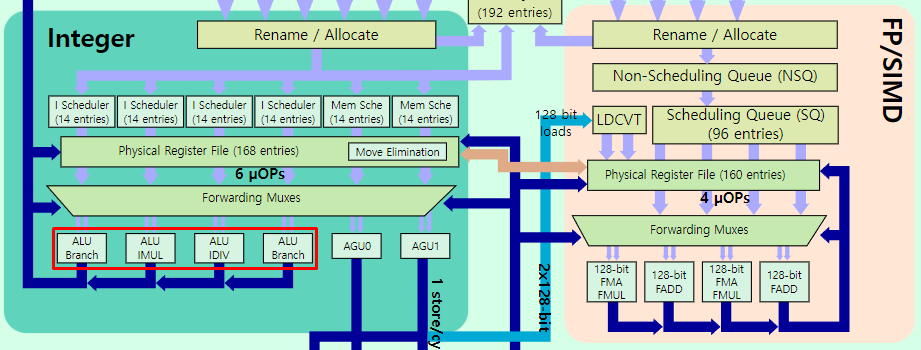
출처: wikichip.org

그런데 감산기도 있는 것을 보고나니 컴퓨터가 덧셈만 가능하다는 것은 틀린 말 같습니다. 옛날 컴퓨터에서 부족한 공간에 하드웨어를 설계하다보니 가산기만 쓰면서 이어져온 이야기가 아닐까 싶습니다. 제가 잘못 이해했을 가능성도…?

여튼, ALU, IMUL, IDIV 등을 내부적으로 어떻게 구현했는지에 따라 사칙연산을 어떻게 하는가가 달라지겠지만, 해당 자료는 검색해도 찾기가 쉽지 않아서 이정도에서 정리하겠습니다.

컴퓨터의 사칙연산에 대한 궁금증을 가지신 분들께 조금이나마 도움이 되었으면 합니다. 잘못된 내용에 대한 지적은 언제나 환영입니다.

참고자료

• Youtube - 컴퓨터는 덧셈 만으로 사칙연산을 할 수 있다!
• 디지털 데일리 - CPU 실행방법… 덧셈·뺄셈·곱셈·나눗셈 어떻게?
• 디지털 데일리 - ALU 구성
• Wikibooks - x86_Assembly
• Wikipedia - ALU
• exclusivearchitecture.com - Arithmetic Logic Unit(ALU)
• Nanyang Technology University - A Tutorial on Data Representation
• Youtube - Binary Addition and Subtraction With Negative Numbers, 2’s Complements & Signed Magnitude
• Youtube - Binary Division Explained (with Examples)
• 모두의 코드 - 컴파일러는 정수 나눗셈을 어떻게 최적화할까?
• gmplib.org - Instruction latencies and throughput for AMD and Intel x86 processors