Union-Find

Posted Sep 22, 2023 Updated Sep 22, 2023

By Seongguk 25 min read

Intro

알고리즘 공부를 하고 싶어서, Coursera 에서 Algorithms, Part1(링크)을 듣기 시작했습니다.

강의의 첫 주제로 배운 Union-Find를 정리해 보겠습니다.

Union-Find

개요

Union-Find는 Disjoint-set 이라고도 합니다.

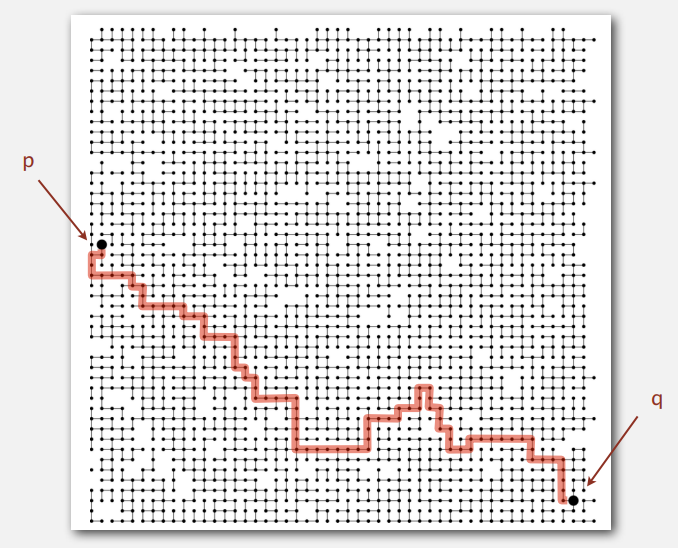
Union-Find의 개념 자체는 크게 어렵지 않습니다. 두 객체 p와 q가 있다고 할 때, 아래와 같이 두 객체를 연결하여 하나로 묶는 것을 Union, 두 객체 p와 q가 연결되어 있는지 찾는 것을 Find라고 합니다.

응용 사례

실생활에서 와닿을 만한 응용 사례로는 Facebook과 같은 소셜 미디어를 생각해볼 수 있습니다. 한 사람을 하나의 객체라고 가정했을 때, 두 사람이 친구가 된다면 Union 연산을 하고, 두 사람이 친구인지 확인하기 위해 Find 연산을 수행합니다. 2023년 Facebook 월간 활성 사용자 수가 대략 30억 명(출처: 링크)이라고 하니, 이러한 상황에서 Union 연산 혹은 Find 연산을 할 때는 속도를 고려하지 않을 수 없을 것입니다.

초당 30억 개의 객체를 순회할 수 있다고 가정할 때, O(n^2) 이라면 최악의 경우 30억 초(대략 10년)가 필요합니다.

수업에서 다루는 문제는 Dynamic Connectivity 문제로 컴퓨터 네트워크에서 응용된다고 합니다.

제가 본 강의에서는 둘이 연결되어 있는지 확인만하는 것을 다루고, 위에서 처럼 경로 찾는 문제는 Part 2 에서 다룬다고 합니다.

Dynamic Connectivity

수업에서는 Dynamic Connectivity가 Union-Find 문제의 추상화된 모델이라고 간단하게 언급하고 넘어가지만, 수업 자료 사이트에서는 아래와 같이 incremental version만 고려하고 있음을 언급하고 있습니다.

Q. Is there an efficient data structure that supports both insertion and deletion of edges?
A. Yes. However, the best-known fully dynamic data structure for graph connectivity is substantially more complicated than the incremental version we consider. Moreover, it’s not as efficient. See Near-optimal fully-dynamic graph connectivity by Mikkel Thorup.

incremental version은 또 무엇인가 의문이 생기게 됩니다.

Wikipedia를 살펴보면, Dynamic Connectivity는 아래와 같이 Edges를 추가만 가능한 경우, 삭제만 가능한 경우, 그리고 둘 다 가능한 경우가 있음을 언급합니다.

The set V of vertices of the graph is fixed, but the set E of edges can change. The three cases, in order of difficulty, are:
Edges are only added to the graph (this can be called incremental connectivity);
Edges are only deleted from the graph (this can be called decremental connectivity);
Edges can be either added or deleted (this can be called fully dynamic connectivity).

Union-Find 에서 Union 연산을 하는 것은 그래프 자료 구조로 표현하자면 간선(Edges)을 추가하는 행위로 볼 수 있습니다.

수업에서는 이렇게 추가만 가능한 경우로 한정한 상태에서 배우고 있다는 것을 인지하고 나머지 내용을 살펴보겠습니다.

용어 정리

용어가 중요하게 사용되지는 않지만, 수업 시간에 나온 용어를 간단하게 정리하고 가겠습니다.

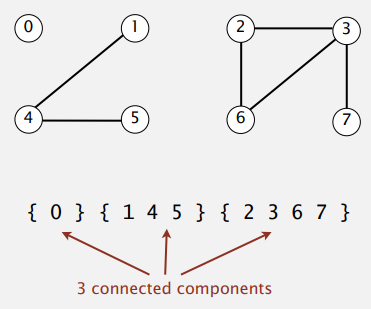
Connected Components

Connected Components 는 다음과 같이 분리된 객체의 집합을 의미합니다. 앞서 Union-Find 를 Disjoint-set 으로 부르기도 한다고 했는데, 좀 더 직관적인 용어라고 볼 수 있겠습니다.

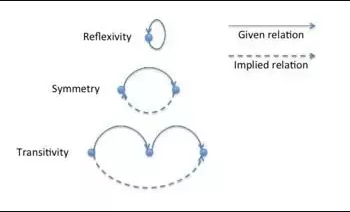
Connected

연결되었다(Connected)는 것의 의미는 아래와 같은 Reflexive, Symmetric, Transitive 성질을 만족하는 것을 의미합니다.

사진 출처: quora.com

그래프로 생각해보면 방향성이 없는 그래프라는 것을 유추해볼 수 있습니다.

다음으로 수업시간에 배우는 Union-Find 문제 해결을 위한 알고리즘을 차례차례 살펴보겠습니다.

Union-Find 구현

강의 자료 사이트에서는 다음 API 문서대로 구현을 하기는 하지만, 수업 시간에는 find와 count를 제외하고, union과 connected만 고려합니다.

Quick Find(Eager Approach)

먼저 Quick Find 입니다. Quick Find는 말 그대로 Find를 빠르게 하는 알고리즘이며, Union은 비효율적으로 처리합니다.

Quick Find 는 Union 연산을 수행하면 바로 해당 Connected Components를 모두 업데이트하여 Eager Approach 의 한 예라고 할 수 있습니다.

먼저 연결되지 않은 상태를 아래와 같이 배열을 통해 표현할 수 있습니다.

그리고 union 연산을 하면 아래와 같이 배열을 업데이트 합니다.

마찬가지로 2와 3을 union 한다면, 아래와 같이 업데이트 합니다.

총 3개의 Connected Components 가 생성되었습니다.

여러개의 객체가 있는 Connected Components 중 일부를 union 연산한다면 아래와 같이 한 쪽의 값으로 업데이트 합니다. 이를 평평한 트리 구조라고 생각하고, 왼쪽 인수로 넣은 객체를 오른쪽 인수로 넣은 객체의 밑으로 들어간다고 생각하면 조금 더 이해하기 쉽습니다.

그리고 연결되어있는지 확인하는 connected 연산을 통해 연결 여부를 판단할 수 있습니다.

Java 코드로 나타내면 아래와 같습니다.

  
public class QuickFindUF {
    private int[] id;
    public QuickFindUF(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++)
        id[i] = i;
    }

    public boolean connected(int p, int q) { return id[p] == id[q]; }

    public void union(int p, int q) {
        int pid = id[p];
        int qid = id[q];
        for (int i = 0; i < id.length; i++)
            if (id[i] == pid) id[i] = qid;
    }
}

연결 여부를 파악(connected/find)할 때는 배열 값을 비교하면 되므로 시간복잡도가 O(1)이 되어, 이름처럼 빠르게 Quick Find 할 수 있습니다.

하지만 union 시에는 배열을 모두 순회하므로, 한 객체 당 다른 객체를 한 번씩 union하는 최악의 경우 시간복잡도가 O(n^2)이 됩니다.

다음으로 Quick Union을 보겠습니다.

Quick Union(Lazy Approach)

Quick Union은 Quick Find와 달리 Lazy Approach의 한 예라고 할 수 있습니다.

앞선 Quick Find가 높이를 1로 유지하는 트리였다면, Quick Union은 높이가 1 이상인 트리라 생각해볼 수 있습니다. Union 시에 첫번째 인수로 사용한 객체의 루트 객체를 두번째 인수로 사용한 객체의 루트 객체로 연결하기만 하면 됩니다. 즉, 두 Connected Components를 합치려면 하나의 루트를 다른 Connected Components의 루트에 연결하기만 하면 됩니다. 그리고 두 객체의 연결 여부를 판단할 때는 루트가 같은지를 Find 명령이 떨어졌을 때 순회하여 찾으면서 판단하므로 Lazy하다고 할 수 있습니다.

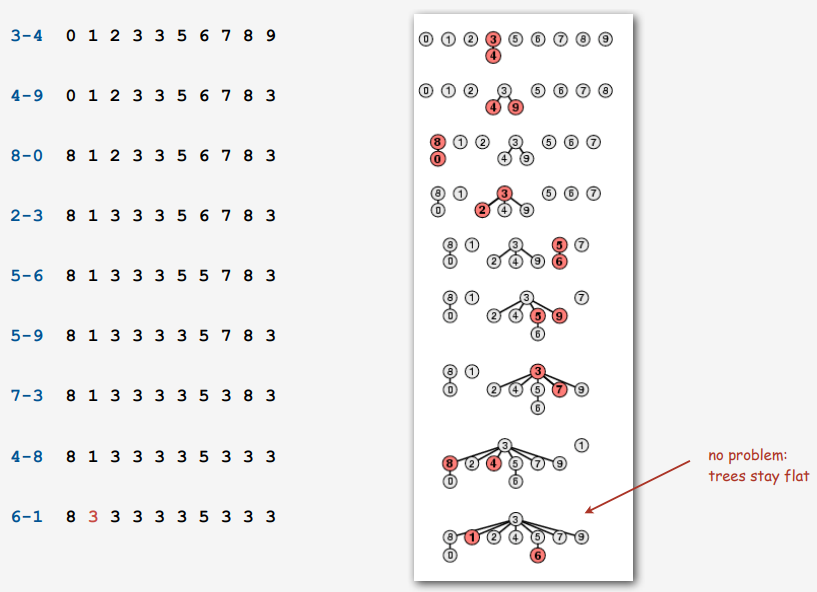
그림으로 보는게 좋겠죠? 이번에는 트리 구조가 어느정도 보여야 하니 갯수를 좀 늘려보겠습니다.

먼저 마찬가지로 union(0, 1)을 해보면 아래와 같이 표현할 수 있습니다.

트리로 상상한 멘탈 모델에서는 달라졌지만, 배열 값을 볼때는 Quick Find와 다른게 없어 보입니다. 하지만, 계속 진행해보면, 다음과 같이 union(1, 3)을 했을 때 1은 3으로 업데이트가 되지만, 0은 업데이트되지 않습니다.

더 진행해 보기 위해서 5와 6을 먼저 union 합니다.

그리고 union(5, 0)를 해보면, 5의 루트인 6이 0의 루트인 3으로 변경됩니다.

이를 구현하기 위해서는 index 값과 배열의 값이 같지 않을 때 루트를 찾아가는 작업이 추가로 필요합니다.

Java로 구현한 Quick Union 코드를 보시면, 아래와 같습니다.

  
public class QuickUnionUF {
    private int[] id;
    public QuickUnionUF(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }

    private int root(int i) {
        while (i != id[i]) i = id[i];
        return i;
    }

    public boolean connected(int p, int q) {
        return root(p) == root(q);
    }

    public void union(int p, int q) {
        int i = root(p);
        int j = root(q);
        id[i] = j;
    }
}

union 은 루트를 찾아서 루트를 변경하고, connected도 루트가 같은지 확인하기 위해 루트를 찾고 있는 것을 볼 수 있습니다.

항상 루트를 찾아야하므로 union, connected 모두 트리의 높이가 연산 속도를 결정하게 됩니다. 사향 이진 트리(Skewed Binary Tree)와 같은 최악의 경우를 생각해보자면, Quick Union에서는 union, find 모두 루트를 찾아야하므로 Quick Find 보다 효율이 더 떨어져 보입니다.

그럼 Quick Find가 더 나은게 아닌가 싶지만, Quick Union은 개선의 여지가 있습니다.

Quick Union은 앞서 이야기했던대로 트리의 높이가 효율성을 결정짓는 주된 요소이므로, 트리의 높이 증가 속도를 낮춰 효율성을 개선합니다.

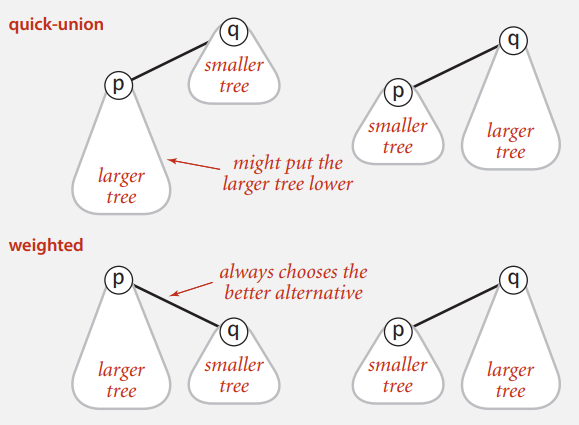
Weighted Quick Union

Quick Union 사용 시 트리의 높이가 너무 높아지는 것을 막기 위해서 항상 작은 트리가 큰 트리의 밑으로 들어가게 합니다.

여기서 크기가 작다 크다는, 트리의 높이가 아닌 포함된 객체의 갯수를 의미합니다.

아래 예제를 보시면, 크기가 작은 트리가 크기가 크거나 같은 트리 밑으로 들어가는 것을 볼 수 있습니다.

Quick Union의 코드를 다시 수정해서, Weighted Quick Union으로 만들어보겠습니다. 트리의 크기를 저장하는 size[] 배열이 추가되고, size[] 배열에 저장된 값에 따라 어떤 Connected Components가 밑으로 들어가게 될지 달라지게 합니다.

  
public class WeightedQuickUnionUF {
    private int[] id;
    private int[] size;
    public WeightedQuickUnionUF (int N) {
        id = new int[N];
        size = new int[N]
        for (int i = 0; i < N; i++) {
            id[i] = i;
            size[i] = 1; // Connected Components의 크기를 모두 1로 초기화
        }
    }

    private int root(int i) {
        while (i != id[i]) i = id[i];
        return i;
    }

    public boolean connected(int p, int q) {
        return root(p) == root(q);
    }

    public void union(int p, int q) {
        int i = root(p);
        int j = root(q);
        // Connected Components의 크기를 비교하고
        // 작은 Connected Components의 루트가 큰 Connected Components 루트 밑으로 이동
        // 그리고 큰 Connected Components의 크기 증가
        if (size[i] < size[j]) { id[i] = j; sz[j] += sz[i]; }
        else                   { id[j] = i; sz[i] += sz[j]; } 
    }
}

크기가 같을 때는 어느 쪽으로 들어가든 상관 없으므로 별도의 처리를 하지 않습니다.

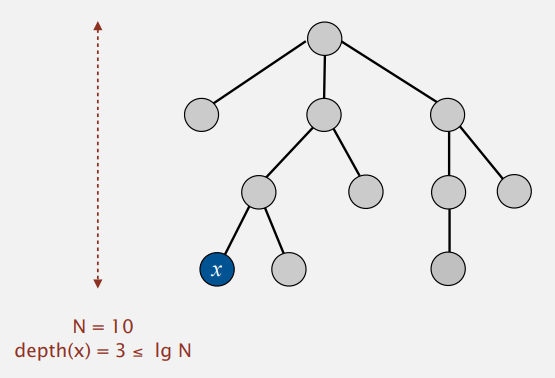
여전히 Quick Union 이므로, O(트리의 높이)가 되는건 마찬가지지만, 트리의 높이는 최대 Log_2(N)을 초과할 수 없음을 수학적으로 증명가능합니다.

Log_2는 base가 2인 Log를 의미합니다.

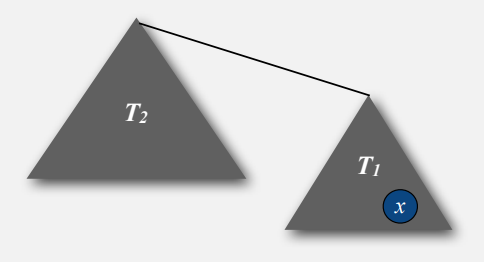
수학적으로 증명하기 위해 먼저 트리 T1과 T2 2개가 있다고 가정합니다.

그림에서 x가 속해있는 T1이 T2에 포함될 때, T2 루트에 의해 밀려나므로 x 의 깊이는 1 증가합니다. 이때 T1을 포함하게되는 T2의 크기는 최소한 T1과 같거나 더 커야합니다. 따라서 T1 크기의 최대값은 T2 크기와 같으므로, T1의 크기는 T2와 병합 결과 최소 2배 증가하고, x의 깊이는 1 증가합니다.

1을 Log_2(N) 번 만큼 2배를 하면 N 이므로, 트리의 크기가 1에서 N이 되려면 (크기는 최소 2배 증가하므로)최대 Log_2(N) 번 병합을 수행해야 합니다.

2^(Log_2(N)) = N

트리의 크기가 1인 트리의 높이가 병합 마다 최대치인 1씩 증가한다고 하면, Log_2(N)번 1씩 높이가 증가하게 되므로, 높이의 최대값은 Log_2(N)이 됩니다.

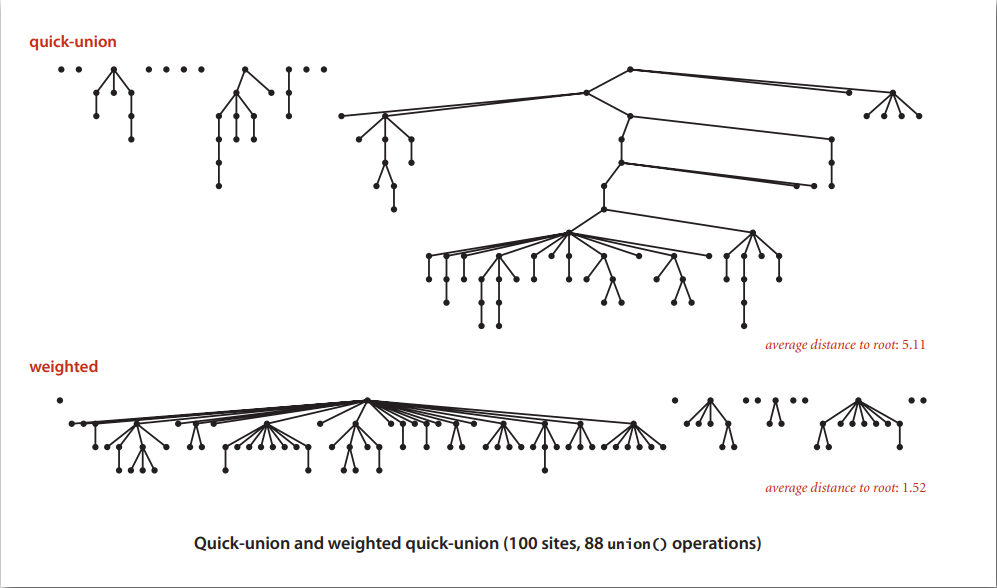
이처럼 Weighted Quick Union은 트리의 높이를 제한하여 성능을 향상시킵니다.

아래 시뮬레이션 결과 예제를 보면, 높이 차이가 많이 나는 것을 볼 수 있습니다.

다른 방법도 있습니다. Path Compression을 Quick Union에 추가한 방식입니다.

Quick Union with Path Compression

지금까지 본 Quick Union 알고리즘은 루트를 찾아갈 때 부모 노드를 하나씩 거슬러 올라가면서 확인합니다.

  
private int root(int i) {
    while (i != id[i]) i = id[i];
    return i;
}

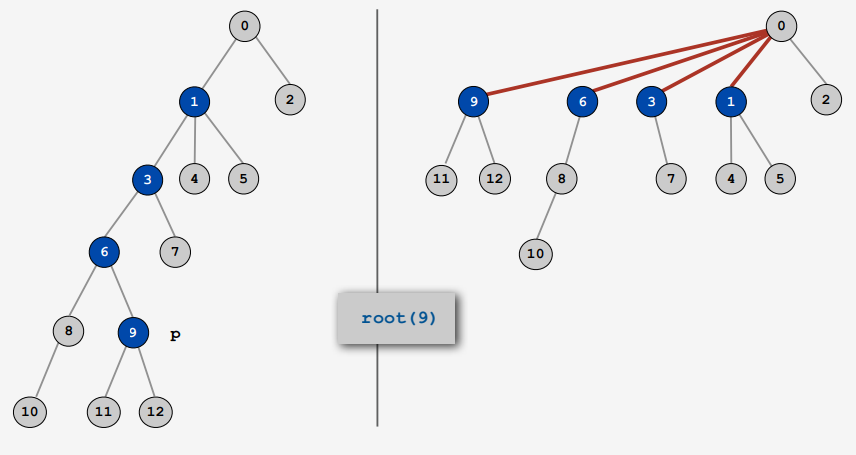
Path Compression은 아래와 같이 9의 루트를 찾을 때, 9를 포함해서 거쳐 가는 객체들이 모두 루트를 가리키게 변경합니다.

이름 답게, Path가 단축됩니다.

이를 구현하기 위한 방식은 여러가지가 있지만, 수업에서 소개된 방식은 할아버지 노드를 가리키게 만들어 Path의 길이를 절반으로 만드는 방식입니다. 코드로 보자면, root 메서드에 id[i] = id[id[i]]; 코드 한 줄을 추가해서 할아버지 노드를 가리키게 합니다.

  
public class QuickUnionWithPathCompressionUF {
    private int[] id;
    public QuickUnionWithPathCompressionUF(int N) {
        id = new int[N];
        for (int i = 0; i < N; i++) id[i] = i;
    }

    private int root(int i) {
        while (i != id[i]) {
            id[i] = id[id[i]];
            i = id[i];
        }
        return i;
    }

    public boolean connected(int p, int q) {
        return root(p) == root(q);
    }

    public void union(int p, int q) {
        int i = root(p);
        int j = root(q);
        id[i] = j;
    }
}

이런식으로 트리를 평평하게 만들어 높이를 낮게 만드는데, 교수님 말씀에 따르면 완전하게 평평하게 만들지는 못해도 실용적인 측면에서 괜찮다고 합니다.

그리고 마지막으로 더 좋은 방법은 가중치를 추가하는 방식과 경로를 압축하는 방식을 모두 사용하는 방법입니다.

Weighted Quick Union with Path Compression

앞의 코드를 같이 사용하면, 아래와 같이 됩니다.

  
public class WeightedQuickUnionWithPathCompressionUF {
    private int[] id;
    private int[] size;
    public WeightedQuickUnionWithPathCompressionUF (int N) {
        id = new int[N];
        size = new int[N]
        for (int i = 0; i < N; i++) {
            id[i] = i;
            size[i] = 1;
        }
    }

    private int root(int i) {
        while (i != id[i]) {
            id[i] = id[id[i]];
            i = id[i];
        }
        return i;
    }

    public boolean connected(int p, int q) {
        return root(p) == root(q);
    }

    public void union(int p, int q) {
        int i = root(p);
        int j = root(q);
        if (size[i] < size[j]) { id[i] = j; sz[j] += sz[i]; }
        else                   { id[j] = i; sz[i] += sz[j]; } 
    }
}

이 알고리즘의 시간 복잡도가 더 개선됨을 여러 명문대 교수님들이 힘을 합쳐 증명했는데, 증명이 쉽지않다고 합니다. 그리고 Ackermann 함수라는 것을 사용하면 더 개선할 수도 있다고 합니다.

또한 다른 명문대 교수님들이 모여서 Union-Find 문제는 선형 시간복잡도로 개선할 수 없음을 수학적으로 증명하기도 했다고 합니다.

그래도 Weighted Quick Union with Path Compression이 이론적으로 완벽하게 선형 시간복잡도는 아니지만, 현실 상에서는 선형 시간복잡도를 갖게된다고 합니다.

그리고 저도 현실을 살아가기 위해 Union Find의 이론적인 부분은 일단 여기까지 해두고, 현실적인 코딩테스트 문제를 찾아보려 합니다. Algorithm, part2 강의에서는 더 깊게 다뤄볼 수 있을거라 기대합니다.

Outro

강의자료 사이트에 가면 connected 메서드는 Deprecated로 표시하고, find 메서드를 사용하는 것으로 변경되어 있습니다.

  
// https://algs4.cs.princeton.edu/15uf/WeightedQuickUnionPathCompressionUF.java.html

    /**
     * Returns the canonical element of the set containing element {@code p}.
     *
     * @param  p an element
     * @return the canonical element of the set containing {@code p}
     * @throws IllegalArgumentException unless {@code 0 <= p < n}
     */
    public int find(int p) {
        validate(p);
        int root = p;
        while (root != parent[root])
            root = parent[root];
        while (p != root) {
            int newp = parent[p];
            parent[p] = root;
            p = newp;
        }
        return root;
    }

    /**
     * Returns true if the two elements are in the same set.
     *
     * @param  p one element
     * @param  q the other element
     * @return {@code true} if {@code p} and {@code q} are in the same set;
     *         {@code false} otherwise
     * @throws IllegalArgumentException unless
     *         both {@code 0 <= p < n} and {@code 0 <= q < n}
     * @deprecated Replace with two calls to {@link #find(int)}.
     */
    @Deprecated
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

Union-Find 인데, 직관적인 측면에서도 find 메서드를 사용하는게 더 맞는 것 같기는 합니다.

코딩테스트 해보면서 다시 글 쓸 때는, find 메서드까지 구현한 Weighted Quick Union with Path Compression 코드로도 작성해봐야겠습니다.

그리고 이외에도 여러가지 세부적인 변형이나 추가적인 내용이 많이 보이는데, 하나의 글에서 다 다루기는 힘들어서 기회가 될때 추가적으로 다뤄보겠습니다.

참고 자료

Algorithms

Algorithms Union-Find

This post is licensed under CC BY 4.0 by the author.

Intro

Union-Find

개요

응용 사례

Dynamic Connectivity

용어 정리

Connected Components

Connected

Union-Find 구현

Quick Find(Eager Approach)

Quick Union(Lazy Approach)

Weighted Quick Union

Quick Union with Path Compression

Weighted Quick Union with Path Compression

Outro

참고 자료

Trending Tags